ত্রিকোণমিতি কি ? ত্রিকোণমিতির জন্ম কথা

হায় শিক্ষার্থী বন্ধুরা, 

আশা করি সবাই ভালো আছো । আগে ত্রিকোণমিতিক জ্ঞান কাজে লাগিয়ে জ্যোতির্বিদগণ পৃথিবী থেকে দূরবর্তী গ্রহ নক্ষত্রের দূরত্ব নির্ণয় করতেন। আধুনিক ত্রিকোণমিতি শুধু জ্যামিতির সাথেই সম্পর্কিত নয় ।এখন এটি গণিতের অন্যান্য শাখাগুলোর সাথেও সমানভাবে সম্পর্কিত হয়ে পড়েছে । 

ত্রিভুজ সংক্রান্ত সমস্যার সমাধান, নেভিগেশন ইত্যাদি ক্ষেত্রে  ত্রিকোণমিতির ব্যাপকব্যাবহার হয়ে থাকে । এছাড়াও জ্যোতির্বিজ্ঞান, ক্যালকুলাস সহ গণিতের গুরুত্বপূর্ণ শাখায় ত্রিকোণমিতির ব্যবহার রয়েছে । 

তাই গণিতের অন্যান্য শাখা সম্পর্কে জ্ঞান অর্জন করতে ত্রিকোণমিতির বিকল্প নেই । আশা করি সংক্ষিপ্ত, এবং ত্রিকোণমিতির এই প্রাথমিক আলোচনার মাধ্যমে ত্রিকোণমিতি কি  সেটি কিছুটা হলেও বুঝতে পারবে ।

ত্রিকোণমিতি কি

ত্রিকোণমিতি কি

চিত্র: ১ △ABC সমকোণী ত্রিভুজে দুটি বাহুর মান AB=3 এবং BC=4 দেওয়া আছে । এখন পিথাগোরাসের বিখ্যাত উপপাদ্য "সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্র অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রের সমষ্টির সমান ।" এর মাধ্যমে অপর বাহু BC এর মান নির্ণয় করা যাবে

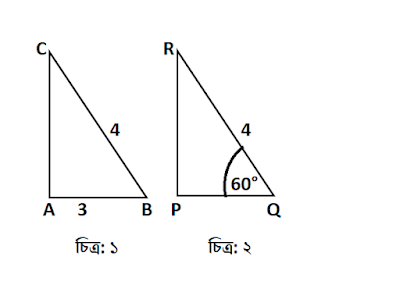
কিন্তু চিত্র: ২ লক্ষ্য কর এখানে △PQR সমকোণী ত্রিভুজের একটি বাহুর মান QR=4 এবং একটি সূক্ষ্মকোণ ∠PRQ=60° দেওয়া আছে  । এখন ঠিক একই পদ্ধতিতে △PQR হতে PR এর মান নির্ণয় করা যাবে না । △PQR হতে যে প্রক্রিয়ায় PR এর মান নির্ণয় করেত হবে সেটির নামই হলো ত্রিকোণমিতি ।

সাধারণ ভাবে বলা হয় ত্রিকোণমিতি হলো গনিতের এমন একটি শাখা যাতে ত্রিভুজের কোণ বাহু ও তাদের মধ্যকার সম্পর্ক ব্যবহার করে বিভিন্ন সমস্যার সমাধান করা যায় ।

আমরা জানি যে কোন ত্রিভুজের তিন কোণের সমষ্টি ১৮০° । কাজেই সমকোণী ত্রিভুজের সমকোণ ব্যাতিত অপর দুই কোণের সমষ্টি ৯০° । এখন ত্রিভুজের তিনটি কোণের পরিমাপ জানা থাকলে এদের বাহুত্রয়ের পরিমাপ নির্ণয় করা যায় । আবার যে কোন এক বাহুর পরিমাপ জানা থাকলে বাকী বাহুর দৈর্ঘ্য জানা যায় । যে প্রক্রিকায় সমকোণী ত্রিভুজের বাহু হতে কোণ, কোণ হতে বাহুর মান নির্ণয় করা যায় সেটিই হলো ত্রিকোণমিতি ।

ইংরেজী শব্দ Trigonometry এর বাংলা প্রতিশব্দ ত্রিকোণমিতি । ইংরেজী শব্দ Trigonometry আবার গ্রিক শব্দ "trigōnon" ত্রিভুজ ও "metron" পরিমাপ থেকে এসেছে । অর্থ্যাৎ শাব্দিক অর্থে বলা যায় ত্রিকোণমিতি অর্থ ত্রিভুজের পরিমাপ ।

পিথাগোরাসের বিখ্যাত উপপাদ্য দ্বারা সমকোণী ত্রিভুজের তিনটি বাহুর মধ্যে সম্পর্ক নিরূপন করা হলেও ত্রিকোণমিতির বিশেষত্ব হলো ত্রিকোণমিতির অনুপাত এবং ত্রিকোণমিতির অভেদ গুলোর মাধ্যমে সমকোণী ত্রিভুজের বাহুর সাথে কোণ, কোণের সাথে বাহুর সম্পর্ক নিরূপন করা যায় । 

আরো পড়তে পারো

 ত্রিকোণমিতি সৃজনশীল প্রশ্ন (৯.১ এবং ৯.২)

ত্রিকোণমিতিক অনুপাত কাকে বলে

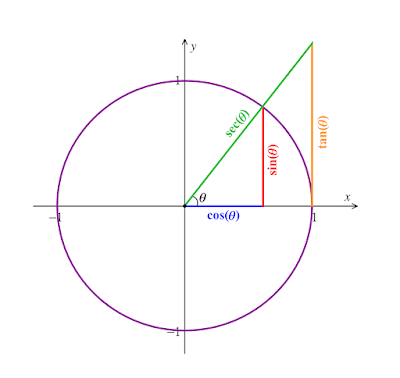
সমকোণী ত্রিভুজের যে কোন একটি সূক্ষকোণের বিপরীতে বাহুগুলোকে পারস্পরিক অনুপাতের ভিত্তিতে একটি নির্দিষ্ট মান পাওয়া যায় যাকে ত্রিকোণমিতিক অনুপাত বলে । ত্রিভুজের তিনটি বাহুর দুটি দুটি করে অনুপাত করলে মোট ছয় প্রকারের অনুপাত পাওয়া যায়।

মনে করি,

△ABC ত্রিভুজে   ∠BAC = সমকোণ    BC = অতিভুজ     AB = সন্নিহিত বাহু   AC = বিপরীত বাহু

∠ABC = θ

সুতরাং

`\frac{AC}{BC}=\sin\theta`                             

 `\frac{AB}{BC}=\cos\theta`     

        

`\frac{AC}{AB}=\tan\theta`                   

 `\frac{AB}{AC}=\cot\theta`

`\frac{BC}{AB}=\sec\theta` 

 `\frac{BC}{AC}=\cosec\theta`

এখন, ∠ABC = θ (সূক্ষ্মকোণ)  সাপেক্ষে উপরোক্ত ত্রিকোণমিতিক ৬ টি অনুপাতের মাধ্যমে সমকোণী ত্রিভুজের যে কোন সূক্ষ্মকোন(θ) দেওয়া থাকলে ত্রিভুজের বাহুগুলোর একটি নির্দিষ্ট মান পাওয়া যায় । যেমন: sinθ=√3/2 । 

আরো পড়তে পারো

সহজে ত্রিকোণমিতির মান মনে রাখার কৌশল

এই মান গুলোর মাধ্যমে বিভিন্ন সমস্যা সমাধান করা যায় ।মনে কর তুমি মিশরে পিরামিড দেখার জন্য গিয়েছ সেখানে গিজায় অবস্থিত খুফুর পিরামিড দেখে সেটির উচ্চতা নির্ণয় করতে চাচ্ছ ।

এখন তোমাকে করতে হবে কি তুমি যেখানে দাড়িয়ে আছ সেখান থেকে পিরামিডের দূরত্ব বের করেত হবে এবং তোমার থেকে পিরামিডের একটি উন্নতি কোন বের করতে হবে যার মাধ্যমে পিরামিডের উপরে না চড়ে নিচ থেকে সহজেই তুমি ত্রিকোণমিতিক জ্ঞান কাজে লাগিয়ে পিরামিডের উচ্চতা বের করতে পারবে । সমস্যাটি ভালো করে বুঝার জন্য নিচের চিত্রটি খেয়াল কর ।

মনে কর PQ হলো পিরামিড । তুমি দাড়িয়ে আছ পিরামিড থেকে 4 মিটার দূরে  R বিন্দুতে । R বিন্দু থেকে পিরামিডের উন্নতি কোণ ∠PRQ=60° । এখন যেহেতু RQ হলো θ কোণ এর সন্নিহিত বাহু এবং  PQ হলো বিপরীত বাহু সুতরাং সমস্যা টি ত্রিকোণমিতিক অনুপাত sinθ এর মাধ্যমে সমাধান করা যাবে । চাইলে সমস্যাটির সমাধান করে আমাকে কমেন্টের মাধ্যমে জানাতে পার। চল এখন জেনে আসি ত্রিকোণমিতির জন্ম হলো কীভাবে ?

ত্রিকোণমিতির জন্ম কথা

গণিতের অন্যান্য শাখাগুলোর মতোই ত্রিকোণমিতিও ইতিহাসের বিভিন্ন বাক পরিবর্তন করে আজকের অবস্থায় পৌঁছেছে । আজকে আমরা যাকে ত্রিকোণমিতি বলে জানি তা আলজাব্রার সাথে সংশ্লিষ্ট । যাকে আধুনিক ত্রিকোণমিতিও বলা যেতে পারে । আধুনিক ত্রিকোণমিতির জন্ম অষ্টাদশ শতকের আগে নয় । 

অন্যদিকে ত্রিকোণমিতির যে শাখাটি জ্যামিতির সাথে সম্পর্কিত সেটির জন্ম আরো আগে । সেটি প্রায় খ্রিষ্টপূর্ব দুইশ বছর আগে গ্রিক জ্যোতির্বেত্তা আর গাণিতিকদের আমলে । যদি ত্রিকোণমিতিকে তিন কোণের পরিমাপ বিদ্যা ধরা হয় তাহলে তার জন্ম আরো আগে সেটি খ্রিস্টপূর্ব দুই হাজার বছরের কাছাকাছি কোন এক সময় ।

১৫৯৫ খ্রিষ্টাব্দে পিটিসকাস নামক একজন গণিতজ্ঞ সর্বপ্রথম ত্রিকোণমিতি নামটি ব্যবহার করেন । পিরামিডের গঠন থেকে বুঝা যায় ত্রিকোণমিতিক জ্ঞানের জন্ম মিশরে । মিশরীয়রা ভূমি জরিপ ও প্রকৌশল কাজে এর ব্যাপক ব্যবহার করতো বলে ধারণা করা হয় । তবে গ্রিক জ্যোতির্বিদ হিপার্কাস (Hipparchus) কে ত্রিকোণমিতির আদি উদ্ভাবক বলে ধরা হয় । 

তবে হিপার্কাস এর পূর্বে খ্রিস্টপূর্ব ২৮০ সালে স্যামস এর অধিবাসী গ্রিক গণিতজ্ঞ আরিস্টার্কাস এর লেখা ''চন্দ্র ও সূর্যের আয়তন ও দূরত্ব'' নামক বইয়ে সর্বপ্রথম ত্রিকোণমিতির ব্যবহার লক্ষ্য করা যায়।আরিস্টার্কাসই সর্বপ্রথম বলেন, নিশ্চল তারাগুলো অনড়, সূর্যও অনড়, পৃথিবী সূর্যের চারদিকে বৃত্তাকার কক্ষপথে ঘোরে । আর সূর্য পৃথিবীর কক্ষ-বৃত্তের কেন্দ্রে অবস্থিত । 

আরো পড়তে পারো

 উপপাদ্য সৃজনশীল : ব্যবহারিক জ্যামিতি 

অর্থ্যাৎ আরিস্টার্কাসই সর্ব প্রথম পৃথিবী সূর্যের চারদিকে ঘোরে এ সত্য আবিষ্কার করেন ।আঠারশত বছর পর ১৫৪৩ খ্রিস্টাব্দে জার্মান বিজ্ঞানী কোপার্নিকাস সর্বপ্রথম তার রচিত দি রেভলিউসনিবাস অরবিয়াম কোয়েলেস্তিয়াম বইয়ের মাধ্যমে এ সত্যকে  বৈজ্ঞানিক ভাবে সুপ্রতিষ্ঠিত করেন । 

সে যাই হোক আরিস্টার্কাস যে প্রক্রিয়ায় পৃথিবী সূর্যের চারদিকে ঘোরে এ সত্য আবিষ্কার করেছিলন তা থেকেই প্রকৃত ত্রিকোণমিতির সূচনা হয়েছিল বলে ধরে নেওয়া যায় ।আরিস্টার্কাস এর কাছ থেকে যে আভাস পাওয়া গিয়েছিল তা আর একটু স্পষ্ট করেন হিপার্কাস (Hipparchus) । 

তিনি  গ্রহ-নক্ষত্র ও তাদের মধ্যবর্তী বেগ এবং দুরত্ব নির্ণয় ও বিচার করতে গিয়ে ত্রিকোণমিতিক জ্ঞানকে আরো প্রসারিত করেন । হিপার্কাস ত্রিকোণমিতিক জ্ঞান ব্যবহার করে প্রায় আটশো স্থির নক্ষত্রের তালিকা বা ক্যাটালগ প্রণয়ন করেন । এই ক্যাটালগে প্রত্যেকটি তারার অবস্থান আকাশ গোলকের উপরকার কৌণিক দূরত্ব দিয়ে বর্ণিত হয়েছে । বর্মানে আমরা যাকে অক্ষাংশ ও দ্রাঘিমাংশ বলি এ ঠিক তার মতোই ।এরপর আসা যাক টলেমির কথায় । 

টলেমি

ইনি আনুমানিক ১০০০ খ্রিষ্টাব্দে জীবিত ছিলেন । Elements গ্রন্থের মাধ্যমে জ্যামিতিতে ইউক্লিড যে অবদান রেখেছিলেন ত্রিকোণমিতিতে টলেমিও সিন্ট্যাক্সিস (Syntaxis) নামক একটি বইয়ের মাধ্যমে সেই একই পরিমান অবদান রেখেছিলেন । 

তিনি ত্রিকোণমিতির সমুদয় জ্ঞানকে একত্রিত করে ১৩ খন্ডের সিন্ট্যাক্সিস (Syntaxis) নামক  বইটি রচনা করেন । যাকে আরবগণ আল-মাজেস্ট (Al-Majest) অতিশয় সম্মানিত গ্রন্থ নামে আরবী অনুবাদ করেন । এই আরবী আনুবাদ থেকেই ১১৭৫ সালে আল-মাজেস্ট বইয়ের লাটিন অনুবাদ হয় । এটি আবার ১৯১৩ সালে গ্রিক অনুবাদ হয় ।

এ বইয়ে হয়তো টলেমির নিজস্ব দান বেশী ছিল না । কিন্তু তিনি এ বইয়ের মাধ্যমে  ত্রিকোণমিতির সমুদয় জ্ঞানকে শ্রেণিবদ্ধ করে লোকের সামনে তুলে ধরতে পেরেছিলেন ।তবে আমরা বর্তমানে "থেটা" "সাইন" "কস" ''টেন'' ''কট'' ''সেক'' ''কোসেক'' ইত্যাদি দিয়ে যে ত্রিকোণমিতি করে থাকি তার উদ্ভাবন করেন মুসলিম গণিতবিদেরা । নবম খ্রিস্টাব্দে আবদুল্লাহ আল-বাত্তানী গোলক ত্রিভুজের কোসাইন (cos) এর নিয়ম আবিষ্কার করেন । 

দশম খ্রিস্টাব্দে আবুল ওয়াফা আল-বুজানি ত্রিভুজের সাইন (sin) উপপাদ্য প্রবর্তন করেন । বর্তমানে আমরা যাকে সিকান্ট (sec) এবং কোসিকান্ট (cosec) বলি তার আবিষ্কারও আরবীয় গণিতবিদরাই করেন ।ষোড়শ শতাব্দীর শেষের দিকে কোপার্নিকাস এর বন্ধু রেটিকাস (Reticus) সাইন, কস , টেন, কট, সেক, কোসেক এর সাত দশমিক পর্যন্ত শুদ্ধ তালিকা প্রস্তুত করেন । ১৫৭৯ খ্রিস্টাব্দে ভিয়েটা এই তালিকা পরিবর্ধত করে প্রতি মিনিট কোণের মান বের করে প্রকাশ করেন । 

প্রিয় পাঠক কোন মানুষই ভুলের উর্ধ্বে নয় । তাই কোন ভুল হলে ক্ষমা সুন্দর দৃষ্টিতে দেখবেন । ভুলগুলো সম্পর্কে জানাবেন । আপনার মতামত সম্মানের সাথে গ্রহণ করা হবে । 

আরো পড়তে পারো

আইফেল টাওয়ার প্রতি বছর ১৫ সে.মি বৃদ্ধি পায় কেন ?